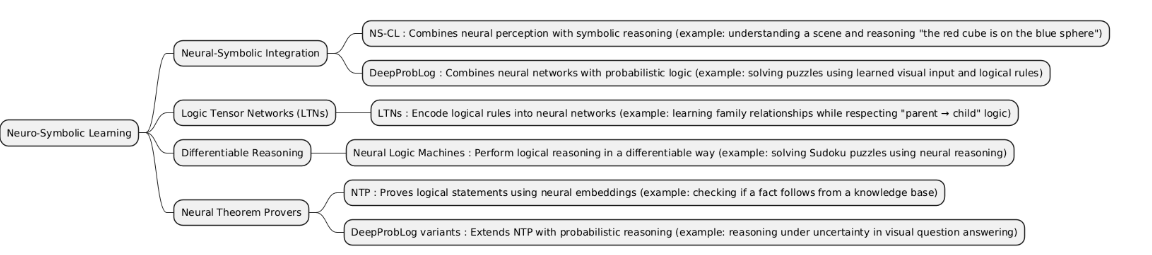
Neuro-Symbolic Learning is an approach that combines neural networks with symbolic reasoning. It leverages the pattern recognition power of neural networks and the logic-based reasoning of symbolic AI to solve complex problems that require both learning from data and understanding structured knowledge.
| Type | What it is | When it is used | When it is preferred over other types | When it is not recommended | Examples of projects that is better use it incide him |
|---|---|---|---|---|---|
| Neural-Symbolic Integration | Neural-Symbolic Integration is a Neuro-Symbolic Learning approach that combines neural networks with symbolic reasoning, allowing models to learn from data while incorporating logical rules and knowledge. | Used when tasks require both pattern recognition (from neural networks) and structured reasoning (from symbolic logic), e.g., complex decision-making or knowledge-based inference. |
• Better than Logic Tensor Networks or Differentiable Reasoning when a general integration of neural and symbolic methods is needed. • More flexible than Neural Theorem Provers for combining learned features with symbolic knowledge in various tasks. |
• When only pattern recognition is needed — pure neural networks (CNNs, Transformers) suffice. • When the domain has little prior knowledge to encode as rules. • When training efficiency is critical — neuro-symbolic models can be slower. |
• Visual question answering — combining image understanding with logic-based reasoning. • Medical diagnosis support — combining patient data with medical knowledge rules. • Robotics — planning actions using learned perception and symbolic reasoning. • Knowledge graph reasoning — inferring missing relations using data and rules. |
| LTNs | Logic Tensor Networks (LTNs) are Neuro-Symbolic Learning models that combine first-order logic with tensor-based neural networks, allowing logical constraints to guide learning and inference. | Used when tasks require learning from data while strictly enforcing logical rules, e.g., relational reasoning or structured knowledge representation. |
• Better than Neural-Symbolic Integration when formal logic constraints are critical and need tensor-based optimization. • More structured than Differentiable Reasoning, focusing on logic-grounded neural learning. • More suitable than Neural Theorem Provers for continuous-valued data combined with logic. |
• When only pattern recognition is needed — simpler neural networks suffice. • When logical rules are not available or hard to define. • For large-scale problems where tensor-based reasoning is computationally heavy. |
• Knowledge graph completion — inferring missing relationships with logical constraints. • Relational reasoning in AI systems with structured rules. • Semantic web applications — combining ontologies and data-driven learning. • Medical diagnosis — ensuring learned predictions satisfy medical logic rules. |
| Differentiable Reasoning | Differentiable Reasoning is a Neuro-Symbolic Learning approach that enables logical reasoning to be incorporated into neural networks via differentiable functions, allowing end-to-end gradient-based training. | Used when tasks require combining neural learning with reasoning, such as complex decision-making, relational inference, or reasoning over structured data. |
• Better than Neural-Symbolic Integration when you want fully differentiable reasoning for gradient optimization. • More flexible than Logic Tensor Networks when strict first-order logic is not required. • Easier to train than Neural Theorem Provers because it uses standard gradient descent. |
• When logical rules are hard to express differentiably. • When reasoning is purely symbolic and interpretability is critical — traditional symbolic methods may be better. • For purely pattern recognition tasks — standard neural networks suffice. |
• Relational question answering — reasoning over structured knowledge. • Robotics planning — integrating learned perception with reasoning for decision-making. • Knowledge graph reasoning — predicting relations while allowing gradient-based training. • Scientific discovery — inferring structured relations from experimental data. |
| NTPs | Neural Theorem Provers (NTPs) are Neuro-Symbolic Learning models that combine neural networks with symbolic logic proving, enabling the system to learn representations of facts and rules and perform logical inference. | Used when tasks require symbolic reasoning over structured knowledge and learning embeddings for facts and rules simultaneously. |
• Better than Neural-Symbolic Integration when formal theorem proving is required alongside neural embeddings. • More structured than Differentiable Reasoning for tasks that need discrete logical proofs. • Preferred over Logic Tensor Networks when explicit deductive reasoning rather than just rule-guided learning is the goal. |
• When only pattern recognition is needed — simpler neural networks suffice. • When rules or knowledge base is incomplete, NTPs may struggle. • For tasks where fast training is required — NTPs can be computationally heavy. |
• Knowledge base completion — inferring missing facts in large knowledge graphs. • Question answering — reasoning over facts with logical proofs. • Mathematical theorem proving — assisting in formal logic proofs. • Ontology reasoning — verifying consistency and deducing new relationships in semantic data. |
from deepproblog.model import Model
from deepproblog.network import Network
from deepproblog.dataset import Dataset
from deepproblog.query import Query
import torch
import torch.nn as nn
class SimpleNN(nn.Module):
def __init__(self):
super().__init__()
self.fc = nn.Linear(2, 10)
def forward(self, x):
return torch.softmax(self.fc(x), dim=-1)
net = Network(SimpleNN(), "digit_net", batching=True)
model_str = """
nn(digit_net, [X1,X2], Digit) :: digit(Digit, [X1,X2]).
sum_correct(A,B,C) :- digit(A,[X1,_]), digit(B,[_,X2]), C is A+B.
"""
model = Model(model_str)
model.add_network(net)
X_train = [torch.tensor([1.0,2.0]), torch.tensor([3.0,4.0]), torch.tensor([2.0,5.0])]
queries = [
Query("sum_correct(1,2,3)"),
Query("sum_correct(3,4,7)"),
Query("sum_correct(2,5,7)")
]
dataset = Dataset(list(zip(X_train, queries)))
model.train(dataset, epochs=10)
result = model.solve(Query("sum_correct(A,B,C)"))
print("Query result:")
print(result)
import torch
import torch.nn as nn
import torch.optim as optim
X = torch.tensor([
[1, 1],
[1, 0],
[0, 1],
[0, 0]
], dtype=torch.float)
y = torch.tensor([
[1, 1, 1],
[1, 0, 0],
[0, 1, 0],
[0, 0, 0]
], dtype=torch.float)
class NSCLNet(nn.Module):
def __init__(self):
super().__init__()
self.fc = nn.Linear(2, 3)
def forward(self, x):
return torch.sigmoid(self.fc(x))
model = NSCLNet()
criterion = nn.BCELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
for epoch in range(500):
optimizer.zero_grad()
outputs = model(X)
loss = criterion(outputs, y)
loss.backward()
optimizer.step()
with torch.no_grad():
test_X = torch.tensor([
[1, 1],
[0, 1],
[1, 0]
], dtype=torch.float)
predictions = model(test_X)
print("Predicted concepts/queries probabilities:")
print(predictions)
import torch
import torch.nn as nn
import torch.optim as optim
X = torch.tensor([
[0, 0],
[0, 1],
[1, 0],
[1, 1]
], dtype=torch.float)
y = torch.tensor([
[0],
[0],
[0],
[1]
], dtype=torch.float)
class NeuralLogicMachine(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(2, 4)
self.fc2 = nn.Linear(4, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.sigmoid(self.fc2(x))
return x
model = NeuralLogicMachine()
criterion = nn.BCELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
for epoch in range(500):
optimizer.zero_grad()
outputs = model(X)
loss = criterion(outputs, y)
loss.backward()
optimizer.step()
with torch.no_grad():
predictions = model(X)
print("Predicted AND probabilities:")
print(predictions)
import torch
import torch.nn as nn
import torch.optim as optim
entities = torch.tensor([
[0.0, 1.0],
[1.0, 0.0],
[0.5, 0.5]
])
labels = torch.tensor([
[0, 1, 0],
[0, 0, 0],
[0, 0, 0]
], dtype=torch.float)
class LTN(nn.Module):
def __init__(self, input_dim):
super().__init__()
self.fc = nn.Sequential(
nn.Linear(input_dim*2, 8),
nn.ReLU(),
nn.Linear(8, 1),
nn.Sigmoid()
)
def forward(self, x, y):
xy = torch.cat([x, y], dim=-1)
return self.fc(xy)
model = LTN(input_dim=2)
criterion = nn.BCELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
for epoch in range(500):
optimizer.zero_grad()
preds = torch.zeros_like(labels)
for i in range(len(entities)):
for j in range(len(entities)):
preds[i,j] = model(entities[i].unsqueeze(0), entities[j].unsqueeze(0))
loss = criterion(preds, labels)
loss.backward()
optimizer.step()
with torch.no_grad():
preds = torch.zeros_like(labels)
for i in range(len(entities)):
for j in range(len(entities)):
preds[i,j] = model(entities[i].unsqueeze(0), entities[j].unsqueeze(0))
print("Predicted parent(x,y) truth values:")
print(preds)